Hướng Dẫn Cách Kiểm Định Giả Thuyết Thống Kê Trong SPSS Chi Tiết Nhất

Kiểm định giả thuyết thống kê trong SPSS là một trong những vấn đề quan trọng đối với các nhà nghiên cứu trong quá trình tìm hiểu đặc điểm của tổng thể. Việc xác định các tham số là cực kì cần thiết để khẳng định độ tin cậy trong thống kê. Bài viết dưới đây List AZ sẽ hướng dẫn bạn cách kiểm định giả thuyết thống kê trong Spss kèm ví dụ cụ thể.

1. Kiểm định giả thuyết thống kê trong SPSS là gì?

• Giả thuyết thống kê là một mệnh đề có chân trị, nghĩa là một phát biểu có đúng hoặc sai. 
• Vì vậy, giả thuyết thồng kê không phải là một danh từ/cụm danh từ mà là một câu nhận định.
• Có thể là câu khẳng định, giả sử, nghi ngờ, hay ý kiến về một hiện tượng, quan hệ hay tình huống dự định khảo sát.
• Kiểm định giả thyết thống kê là một phương pháp thống kê suy luận (statistical inference).
• Đây là một phương pháp thống kê mà các nhà nghiên cứu thường lựa chọn để kiểm định một giả thiết cho một hoặc một số tham số quần thể.
• Hiểu một cách đơn giản đây là việc sử dụng thông tin từ mẫu nghiên cứu để suy diễn ra vấn đề của quần thể.
• Kiểm định giả thuyết thống kê chỉ áp dụng với việc nghiên cứu định lượng, phần định tính không sử dụng được phương pháp này.
• Kiểm định giả thuyết thống kê trong SPSS trả lời cho 3 câu hỏi sau:
• Câu hỏi mô tả: Nhằm mô tả hiện tượng

VD: Khách hàng mua hàng ở đâu, Động cơ mua là gì, Khách hàng thích gì ở sản phẩm,…

• Câu hỏi về sự khác biệt: Nhằm so sánh sự khác biệt

VD: 2 nhóm khách hàng khác nhau có lợi ích tìm kiếm, sản phẩm khác nhau không? Cảm nhận về thương hiệu A có khác thương hiệu B không? Khác ở điềm nào? 

• Câu hỏi về sự liên hệ: Xác định mức độ liên hệ của các hiện tượng

VD: Động cơ, thu nhập có ảnh hưởng đến cảm nhận về chất lượng hay không?

• Có 2 loại giả thuyết trong thống kê:

• Giả thuyết không: Là giả thuyết mà ta muốn kiểm định (H0)
• Giả thuyết đối: Giả thuyết ngược lại với giả thuyết không (H1)

VD:

– Giả thuyết không: Không có sự khác biệt giữa tuổi của nam và nữ

 H0: nam = nữ

– Giả thuyết đối: Có sự khác biệt giữa tuổi của nam và nữ

H1: nam ≠ nữ

2. 3 loại kiểm định giả thuyết trong thống kê SPSS

Việc kiểm định một giả thuyết thống kê dựa trên sự phân loại của tham số mà vấn đề, tình huống nghiên cứu đưa ra. Dựa trên những đặc tính của tham số, có thể chia thành 3 loại kiểm định giả thuyết trong thống kê SPSS:

2.1. Kiểm định sự liên quan của 2 biến định tính

• Biến có thang đo danh nghĩa (nominal) hay thứ bậc (ordinal) là biến có thang đo định tính. Để kiếm định sự liên quan giữa hai biến định tính ta dùng kiểm định Chi bình phương (Chi-Square).

Ví dụ: Nhà nghiên cứu khảo sát sự liên quan của giới tính (gender: male/female) và phương tiện học tập ưu tiên (Preferred Learning Medium).

Thực hiện kiểm định Chi bình phương: Đầu tiên nhập data 2 cột Gender và Preferred Learning Medium vào SPSS. Sau đó vào Analyze > Descriptives Statistics > Crosstabs.

Tại cửa sổ Crosstabs đưa biến Gender vào ô Row(s) và biến Preferred Learning Medium vào ô Column(s), có thể đưa một trong hai biến vào bất kỳ mục Rows hay Column đều được, không ảnh hưởng đến kết quả kiểm định. Để hiển thị đồ thị mối quan hệ hai biến, người học có thể chọn vào Display clustered bar charts.

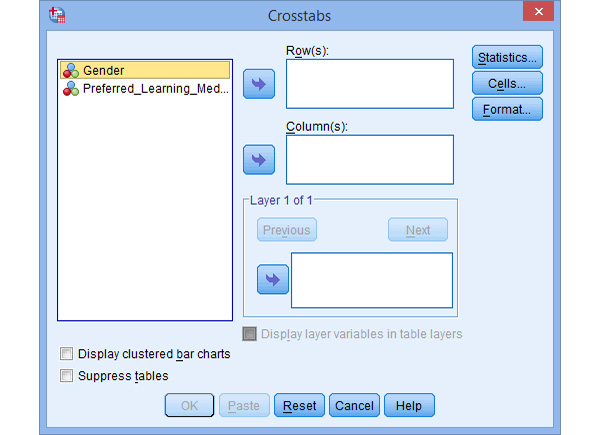
Nhấp vào tùy chọn Statistics, sau đó tick chọn vào Chi-square và Cramer’s V, sau đó nhấp vào Continue. Nhấp vào tùy chọn Cells, trong mục Percentages tích chọn vào Rows, Columns. 

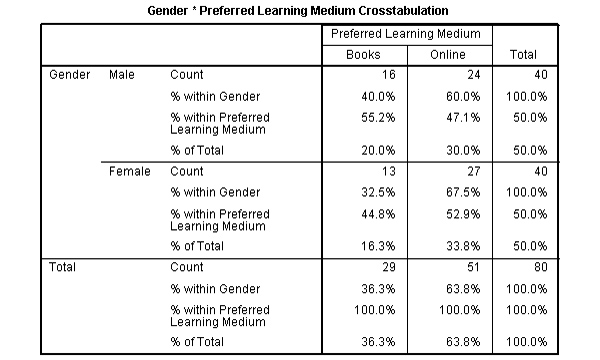
Trong kết quả ở Output, bảng Crosstabulation cho chúng ta cái nhìn sơ bộ về mối quan hệ giữa hai biến này về mặt thống kê tần số.

Tiếp đến, chúng ta sẽ đọc bảng quan trọng nhất là Chi-Square Tests.

• Nếu giá trị Asymptotic Significance (2-sided) hàng Pearson Chi-Square nhỏ hơn 0.05, điều này cho thấy rằng phải bác bỏ giả thuyết Ho, nghĩa là 2 biến Gender và Preferred Learning Medium có mối quan hệ với nhau.
• Nếu giá trị Sig này lớn hơn 0.05, giả thuyết Ho được chấp nhận, đồng nghĩa rằng Gender và Preferred Learning Medium không có mối quan hệ với nhau. 

Cuối bảng Chi-Square Tests luôn có một dòng thông báo dạng: X cells (Z%) have expected count less than 5. The minimum expected count is Y. Khi chạy không ra được kết quả kiểm định, các bạn cần để ý đến dòng này. 

• Kiểm định Chi bình phương chỉ có ý nghĩa khi số quan sát đủ lớn, nếu có quá 20% số ô trong bảng Crosstabulation có tần số nhỏ hơn 5 thì Chi-Square không còn mang ý nghĩa chính xác hoặc có thể kết quả kiểm định không thực hiện được và báo lỗi. 
• Khi xảy ra trường hợp này, các bạn cần tăng số lượng người khảo sát ở các nhóm đáp án có dưới 5 người trả lời hoặc mã hóa lại biến để tăng số lượng người ở mỗi đáp án lên đủ lớn.

• Khi đọc bảng này, chúng ta quan tâm đến kết quả của hàng “Pearson Chi-Square”. Ở đây ta có thể thấy rằng χ (1) = 0,487, p = 0,485. Điều này cho chúng ta biết rằng không có mối liên quan có ý nghĩa thống kê giữa Gender và Preferred Learning Medium; nghĩa là cả Nam và Nữ đều thích học trực tuyến hơn sách.

• Phi và Cramer’s V đều kiểm tra độ mạnh của mối liên hệ. Chúng ta có thể thấy rằng độ mạnh liên kết giữa các biến là rất yếu.
• Đồ thị cột biểu diễn tần số người khảo sát của mỗi giá trị của biến này khi so với biến còn lại, đây là đồ thị biểu diễn kết quả bảng Crosstablulation. 

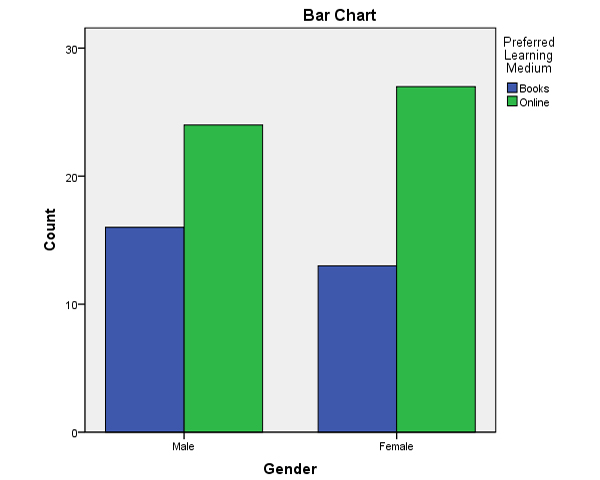
Nhìn vào biểu đồ có thể dễ dàng hình dung dữ liệu hơn là đọc bảng. Có thể tùy chọn biểu đồ để các cột có các biến liên quan với nhau, làm nổi bật các danh mục nhóm và tần suất người khảo sát trong các nhóm này.

Kiểm định Chi bình phương hay còn gọi là kiểm định Crosstab thường được ứng dụng nhiều khi:

• Cần phân tích sâu hơn mối quan hệ giữa các đặc điểm nhân khẩu học của mẫu khảo sát hoặc phân tích sự liên kết các yếu tố trong thị trường… 
• Đây là một công cụ mạnh hỗ trợ chúng ta đưa ra giải pháp cho bài nghiên cứu.

2.2. Kiểm định giả thuyết về trung bình tổng thể

Để tăng chính xác trong phần kiểm định giả thuyết thống kê, người nghiên cứu có thể sử dụng cách kiểm định trung bình tổng thể so với các giá trị khác. Cách kiểm định này gồm 2 loại chính: kiểm định tham số và phi tham số.

2.2.1. Kiểm định tham số

Tùy thuộc vào giá trị trung bình của tổng thể như thế nào, có thể sử dụng 4 cách kiểm định dưới đây:

• Cách kiểm định One sample T – Test: Sử dụng khi giá trị trung bình của một đại lượng (đo bằng thang đo scale) của tổng thễ bằng giá trị C.

• Kiểm định One-Sample T-Test nhằm mục đích so sánh trung bình (mean) của tổng thể với một giá trị cụ thể nào đó. 
• Ví dụ như kiểm tra xem điểm trung bình kỳ thi cuối kỳ của học sinh trong lớp là cao hơn, thấp hơn hay bằng 8 điểm; kiểm tra xem chiều cao trung bình của các ứng viên tham dự cuộc thi Hoa hậu Hoàn Vũ là cao hơn, thấp hơn hay bằng 1,7 mét,..v…v…

Ví dụ: Một nhà nghiên cứu đang lên kế hoạch kiểm tra khảo sát một chỉ số trầm cảm cụ thể, trong đó bất kỳ ai đạt được điểm số 4.0 được coi là có mức độ trầm cảm ‘bình thường’ (normal). Tương tự, điểm thấp cho thấy ít trầm cảm và điểm cao cho thấy trầm cảm nhiều hơn. Ông đã tuyển chọn 40 người tham gia nghiên cứu. Điểm số trầm cảm là biến dep_score. Người nghiên cứu muốn biết liệu mẫu có đại diện cho dân số bình thường hay không (nghĩa là họ có điểm số khác biệt đáng kể về mặt thống kê so với 4,0).

• Đối với thử nghiệm t một mẫu, sẽ chỉ có một dữ liệu của biến được nhập vào Thống kê SPSS: biến phụ thuộc, dep_score là điểm trầm cảm.
• Giả thuyết H0 đặt ra cho kiểm định One-Sample T-Test là: Điểm đánh giá trung bình của người khảo sát đối với các tiêu chí của nhân tố trầm cảm là 4. Chúng ta sẽ thực hiện kiểm định để xem thử sẽ bác bỏ hay chấp nhận giả thuyết Ho (độ tin cậy được sử dụng là 95%).

Thực hiện trên SPSS 20, vào Analyze > Compare Means > One-Sample T Test…

Giao diện cửa sổ One-Sample T-Test xuất hiện, các bạn đưa các biến cần kiểm định vào mục Test Variable(s), cụ thể trong trường hợp này là 0 đến 4. Tiếp đến, nhập giá trị muốn so sánh trung bình vào mục Test Value, cụ thể ở đây 4.

Sau đó nhấp OK, xuất hiện 2 bảng xuất hiện ở file Output. Một bảng là One-Sample Statistics thống kê giá trị trung bình, độ lệch chuẩn các biến; bảng còn lại là One-Sample Test cho biết kết quả kiểm định vừa thực hiện.

• Việc không trình bày thống kê mô tả của bạn bằng cách sử dụng giá trị trung bình và độ lệch chuẩn (cột “Std. Deversion”) thường gặp hơn là sai số chuẩn của giá trị trung bình (cột “Std. Error Mean”), mặc dù cả hai đều có thể chấp nhận được. Bạn có thể báo cáo kết quả, sử dụng độ lệch chuẩn như sau: 
• Điểm số trầm cảm trung bình (M = 3,72, SD = 0,74) thấp hơn điểm số trầm cảm ‘bình thường’ của dân số là 4,0.

• Trong ví dụ này, bạn có thể thấy giá trị điểm trầm cảm ‘bình thường’ là “4” mà bạn đã nhập trước đó. Bây giờ, bạn cần tham khảo ba cột đầu tiên của bảng Kiểm tra một mẫu, bảng này cung cấp thông tin về việc liệu mẫu có phải từ một tập hợp có giá trị trung bình là 4 hay không (tức là các phương tiện này khác nhau có ý nghĩa thống kê),

• Nhìn từ trái sang phải, bạn sẽ thấy giá trị t quan sát được (cột “t”), bậc tự do (“df”) và ý nghĩa thống kê (p-value) (“Sig. (2) đuôi) “) của thử nghiệm t một mẫu. Trong ví dụ này, p <.05 (nó là p = .022). Do đó, có thể kết luận rằng các phương tiện dân số khác nhau có ý nghĩa thống kê. Nếu p > 0,05, sự khác biệt giữa trung bình ước tính mẫu và trung bình dân số so sánh sẽ không khác biệt có ý nghĩa thống kê.

• Cách kiểm định Independent Samples T – Test: Sử dụng khi giả thuyết là giá trị trung bình của một đại lượng (đo bằng thang đo scale) của tổng thể thứ nhất bằng giá trị đó của tổng thể thứ 2.

Ví dụ: Nhà nghiên cứu đã quyết định điều tra xem liệu một bài tập thể dục hoặc can thiệp giảm cân có hiệu quả hơn trong việc giảm mức cholesterol hay không. Để đạt được mục tiêu này, nhà nghiên cứu đã tuyển chọn ngẫu nhiên một mẫu nam giới không hoạt động được phân loại là thừa cân. Mẫu này sau đó được chia ngẫu nhiên thành hai nhóm: Nhóm 1 thực hiện chế độ ăn kiêng (diet group) kiểm soát lượng calo và Nhóm 2 thực hiện chương trình tập luyện-đào tạo (exercise group). Để xác định chương trình điều trị nào hiệu quả hơn, nồng độ cholesterol trung bình được so sánh giữa hai nhóm vào cuối chương trình điều trị.

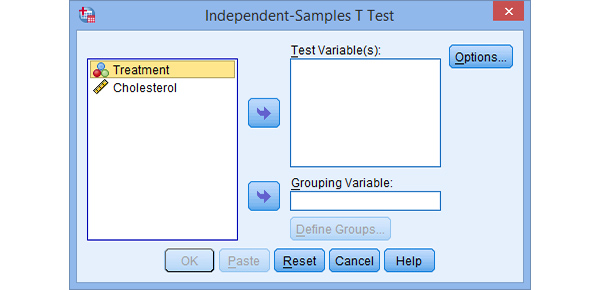
• Ta xác định được 2 biến chính bao gồm: biến treatment (gồm diet group và exercise group) là biến phụ thuộc và biến Cholesterol là biến độc lập.
• Việc thực hiện kiểm định trên Spss như sau: Vào Analyze > Compare Means > Independent Sample T-Test. Ở hộp giao diện, đưa biến treatment vào phần Test Variable (s), đưa biến Cholesterol vào phần Grouping Variable. Ở phần dưới có nút Define Groups, nhấn chọn phần này.

Ở đây có thể thấy biến treatment có 2 giá trị: 1 là diet group, 2 là exercise group, do vậy người học điền 2 số này vào 2 ô trống, có thể điền phần nào trước cũng được. Tiếp theo nhấn vào mục Continue. 

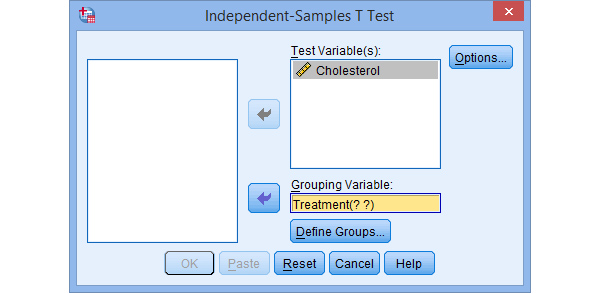
Xuất hiện kết quả của phần kiểm định là bảng sau:

• Bạn có thể thấy rằng các phương tiện của nhóm khác nhau có ý nghĩa thống kê vì giá trị trong hàng “Sig. (2 đuôi)” nhỏ hơn 0,05. Nhìn vào bảng Thống kê Nhóm, chúng ta có thể thấy rằng những người thực hiện thử nghiệm tập thể dục có mức cholesterol thấp hơn vào cuối chương trình so với những người thực hiện chế độ ăn kiêng kiểm soát calo.
• Dựa vào bảng trên, người học có thể báo cáo kết quả nghiên cứu như sau: Nghiên cứu này cho thấy rằng những người tham gia là nam giới thừa cân, không hoạt động thể chất có nồng độ cholesterol thấp hơn có ý nghĩa thống kê (5,80 ± 0,38 mmol / L) khi kết thúc chương trình luyện tập thể dục so với sau chế độ ăn kiêng kiểm soát calo (6,15 ± 0,52 mmol / L), t (38) = 2,428, p = 0,020.

• 2  lưu ý:

• Trường hợp sig nhỏ hơn 0.05:

Trong trường hợp này sẽ ra kết quả là phương sai giữa 2 chương trình giảm cân là khác nhau, do đó sẽ sử dụng giá trị sig T-Test ở hàng Equal variances not assumed. 

– Giá trị sig T-Test < 0.05 chúng ta kết luận: Có sự khác biệt có ý nghĩa thống kê về nồng độ cholesterol của những đáp viên có chương trình giảm cân khác nhau.

– Giá trị sig T-Test >= 0.05 chúng ta kết luận: Không có sự khác biệt có ý nghĩa thống kê về nồng độ cholesterol của những đáp viên có chương trình giảm cân khác nhau.

• Trường hợp sig lớn hơn hoặc bằng 0.05

Trong trường hợp này sẽ ra kết quả là phương sai giữa 2 chương trình giảm cân là khác nhau, tiếp tục phần sig T-Test được sử dụng như trên.

– Nếu sig T-Test < 0.05, kết luận bài nghiên cứu: Có sự khác biệt có ý nghĩa thống kê về nồng độ cholesterol của những đáp viên có chương trình giảm cân khác nhau.

– Nếu sig T-Test >= 0.05 kết luận bài nghiên cứu: Không có sự khác biệt có ý nghĩa thống kê về nồng độ cholesterol của những đáp viên có chương trình giảm cân khác nhau

• Kiểm định Paired sample T – Test: đây là phương pháp kiểm định nhằm so sánh giá trị trung bình giữa hai nhóm liên quan trên cùng một biến phụ thuộc và độc lập. Ví dụ: bạn có thể sử dụng thử nghiệm t phụ thuộc để biết liệu có sự khác biệt trong việc tiêu thụ thuốc lá hàng ngày của người hút thuốc trước và sau chương trình trị liệu thôi miên 6 tuần hay không (nghĩa là, biến phụ thuộc của bạn sẽ là “mức tiêu thụ thuốc lá hàng ngày” và hai biến số phụ thuộc của bạn có liên quan nhóm sẽ là các giá trị tiêu thụ thuốc lá “trước” và “sau” chương trình trị liệu thôi miên). 

3 Lưu ý: 

• Hai mẫu được so sánh phải có kích thước bằng nhau và sự khác biệt giữa các giá trị của hai mẫu phải được phân phối chuẩn, hoặc kích thước mẫu phải đủ lớn để được coi là xấp xỉ của phân phối chuẩn.
• Dữ liệu cho mẫu được thu thập dưới dạng thang đo định lượng Ordinal hoặc Scale. Quy trình thử nghiệm sẽ bắt đầu bằng cách tính toán sự khác biệt cho từng cặp quan sát bằng phép trừ, sau đó kiểm tra xem sự khác biệt trung bình của tổng thể = 0 và nếu = 0 thì không có sự khác biệt nào.
• Ưu điểm của thử nghiệm mẫu theo cặp là loại trừ các ảnh hưởng bên ngoài đối với nhóm thử nghiệm.

Ví dụ: Một nhóm sinh viên Khoa học Thể thao (n = 20) được chọn từ dân số để điều tra xem liệu chương trình đào tạo plyometric 12 tuần có cải thiện thành tích nhảy xa của họ hay không. Để kiểm tra xem liệu việc đào tạo này có cải thiện thành tích hay không, các học sinh được kiểm tra thành tích nhảy xa của họ trước khi họ thực hiện một chương trình đào tạo plyometric và sau đó một lần nữa vào cuối chương trình (nghĩa là, biến phụ thuộc là “thành tích nhảy xa”, và hai nhóm liên quan là giá trị nhảy xa đứng “trước” và “sau” chương trình đào tạo plyometric 12 tuần).

Tiến hành phương pháp kiểm định Paired-Samples T Test: vào Analyze > Compare Means > Paired-Samples T Test. Xuất hiện hộp Paired-Samples T Test, đưa 2 biến JUMP1 (trước khi đào tạo) và JUMP2 (sau khi đào tạo) muốn kiểm định trị trung bình vào phần Paired Variables.

• Chọn độ tin cậy là 95% tại phần tùy chọn Options. Bạn có thể để mức tin cậy từ 90% trở lên tùy vào phương pháp kiểm định.Sau đó chọn Continue, quay lại hộp thoại ban dầu, chọn OK.
• Kết quả Output sẽ có 2 bảng. Bảng xuất hiện đầu tiên là Paired Samples Statistics. Kết quả ở đây được sử dụng để mô tả các đặc điểm của lần khảo sát nhảy thứ nhất và thứ hai trong bài.

• Bảng tiếp theo là Paired Samples Test là nơi trình bày các kết quả của phép thử t phụ thuộc. Nhiều thông tin được trình bày ở đây và điều quan trọng cần nhớ là thông tin này đề cập đến sự khác biệt giữa hai lần khảo sát. Do đó, các cột của bảng có nhãn “Mean“, “Std. Deviation“, “Std. Error Mean” và “95% Confidence Interval of the Difference” đề cập đến sự khác biệt trung bình giữa hai lần nhảy và độ lệch chuẩn, tiêu chuẩn sai số và khoảng tin cậy 95% của sự khác biệt trung bình này, tương ứng. Ba cột cuối cùng biểu thị kết quả của phép kiểm tra t phụ thuộc, đó là giá trị t (“t”), bậc tự do (“df”) và mức ý nghĩa (“Sig. (2 đuôi)”).

• Có thể báo cáo thống kê theo định dạng sau: t (bậc tự do) = t-value, p = mức ý nghĩa. Trong trường hợp của chúng ta, đây sẽ là: t (19) = -4,773, p < 0,0005. Do phương tiện của hai lần nhảy và hướng của giá trị t, chúng ta có thể kết luận rằng đã có sự cải thiện đáng kể về mặt thống kê trong khoảng cách nhảy theo chương trình đào tạo plyometric từ 2,48 ± 0,16 m đến 2,52 ± 0,16 m (p <0,0005 ); cải thiện 0,03 ± 0,03 m.
• Lưu ý: Thống kê SPSS có thể xuất kết quả đến nhiều chữ số thập phân, nhưng bạn nên hiểu thang đo của mình để biết liệu có phù hợp để báo cáo kết quả của bạn với độ chính xác như vậy hay không.

• Cách kiểm định One way novada: Sử dụng khi giả định rằng giá trị trung bình của các số (đo theo tỷ lệ) của một quần thể (có thể là nhiều quần thể) là bằng nhau.

• Anova giúp giải quyết khó khăn trong Independent Sample T-Test. Phương pháp này giúp chúng ta so sánh trị trung bình của 2 nhóm trở lên. 
• Anova chỉ nên sử dụng cho các biến có tính chất định tính.

Ví dụ: Nhà đào tạo cung cấp 3 khóa học: một khóa sơ cấp, trung cấp và cao cấp. Người quản lí không chắc khóa học nào là cần thiết cho loại công việc họ làm tại công ty của mình, vì vậy anh ta cử 10 nhân viên tham gia khóa học sơ cấp, 10 nhân viên trung cấp và 10 nhân viên tham gia khóa học nâng cao. Khi tất cả họ trở về từ khóa đào tạo, anh ấy đưa ra cho họ một vấn đề cần giải quyết bằng chương trình bảng tính và thời gian họ mất bao lâu để hoàn thành bài toán. Sau đó, anh ta so sánh ba khóa học (sơ cấp, trung cấp, cao cấp) để xem liệu có bất kỳ sự khác biệt nào về thời gian trung bình để hoàn thành bài toán hay không.

Chúng ta sẽ có 2 biến chính là course phân thành 3 nhóm beginners, intermediate và advanced và biến time.

Cách thực hiện phân tích kiểm định ANOVA: Vào Analyze > Compare Means > One-Way ANOVA. Giao diện xuất hiện như dưới đây, người học đưa biến Time vào phần Dependent List,ở phần Factor điền biến Course.

Tương tự vào tùy chọn Options như các cách kiểm định trên. Sau đó chọn Continue.và OK để xuất ra Output.

Bảng bạn quan tâm đầu tiên đó là bảng Descriptives cung cấp một số thống kê mô tả rất hữu ích, bao gồm giá trị trung bình, độ lệch chuẩn và khoảng tin cậy 95% cho biến phụ thuộc (Thời gian) cho từng nhóm riêng biệt (Người mới bắt đầu, Trung cấp và Nâng cao), cũng như khi tất cả các nhóm được kết hợp (Tổng số). Những số liệu này hữu ích khi bạn cần mô tả dữ liệu của mình.

Dưới đây là bảng hiển thị kết quả của phân tích ANOVA và liệu có sự khác biệt có ý nghĩa thống kê giữa ý nghĩa nhóm của chúng tôi hay không. Chúng ta có thể thấy rằng giá trị ý nghĩa là 0,021 (tức là p = 0,021), thấp hơn 0,05. và do đó, có sự khác biệt có ý nghĩa thống kê về khoảng thời gian trung bình để hoàn thành bài toán bảng tính giữa các khóa học khác nhau được thực hiện.

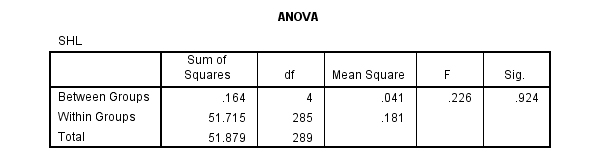
• Nếu sig ở bảng ANOVA < 0.05, chúng ta kết luận: Có sự khác biệt có ý nghĩa thống kê về thời gian hoàn thành bài tập của những đáp viên thuộc các lớp học khác nhau.

• Nếu sig ở bảng ANOVA >= 0.05, chúng ta kết luận: Không có sự khác biệt có ý nghĩa thống kê về thời gian hoàn thành bài tập của những đáp viên thuộc các lớp học khác nhau.
• Từ kết quả này, chúng ta biết rằng có sự khác biệt có ý nghĩa thống kê giữa các nhóm nói chung. Bảng Multiple Comparisons dưới đây cho thấy các nhóm nào khác với nhau.
• Chúng ta có thể thấy từ bảng dưới đây rằng có sự khác biệt có ý nghĩa thống kê về thời gian hoàn thành bài toán giữa nhóm tham gia khóa học sơ cấp và trung cấp (p = 0,046), cũng như giữa khóa học sơ cấp và khóa học nâng cao (p = 0,034). Tuy nhiên, không có sự khác biệt giữa các nhóm học trung cấp và cao cấp (p = 0,989).

Dựa vào kết quả trên, chúng ta có thể đưa ra kết luận như sau: 

• Có sự khác biệt có ý nghĩa thống kê giữa các nhóm được xác định bởi ANOVA một chiều (F (2,27) = 4,467, p = 0,21). 
• Bài kiểm tra cho thấy thời gian hoàn thành bài toán thấp hơn có ý nghĩa thống kê sau khi tham gia khóa học trung cấp (23,6 ± 3,3 phút, p = 0,046) và nâng cao (23,4 ± 3,2 phút, p = 0,034) so với người mới bắt đầu khóa học (27,2 ± 3,0 phút). 
• Không có sự khác biệt có ý nghĩa thống kê giữa nhóm trung cấp và cao cấp (p = 0,989).

Phương pháp kiểm định tham số đối với mẫu trung bình tổng thể là một trong những phương pháp phổ biến khi kiểm định giả thuyết thống kê trong SPSS. Nếu bạn gặp khó khăn trong khi sử dụng các phương pháp này, đội ngũ nhân sự giàu kinh nghiệm của chúng tôi sẽ hỗ trợ bạn một cách tốt nhất trong cách kiểm định t test.

2.2.2. Kiểm định phi tham số

  Trong thống kê, kiểm định phi tham số là phương pháp phân tích thống kê không yêu cầu phân phối chuẩn để đáp ứng các giả định cần thiết được phân tích (đặc biệt nếu dữ liệu không được phân phối chuẩn).

• Phương pháp này còn được gọi là kiểm định không phân phối.
•  Kiểm định phi tham số đóng vai trò thay thế cho các bài kiểm định tham số như T-test hoặc ANOVA chỉ có thể được sử dụng nếu dữ liệu cơ bản đáp ứng các tiêu chí và giả thuyết nhất định.

  Có 3 phương pháp thường đước sử dụng trong kiểm định phi tham số:

• Cách kiểm định Mann Whitney: được dùng để kiểm định các giả thiết về 2 mẫu độc lập không có phân phối chuẩn.

Ví dụ: So sánh nồng độ cholesterol trung bình giữa 2 nhóm: nhóm ăn kiêng (diet group) và nhóm tập thể dục (exercise group) để xem xét phương pháp giảm cân nào có hiệu quả.

Các bước thực hiện kiểm định như sau: Vào Analyze > Nonparametric Tests > 2 Independent Samples. 

Xuất hiện hộp thoại Two-Independent-Samples Tests, nhấn dấu vào ô Mann-Whitney U. Sau đó chuyển Cholesterol vào mục Test Variable List.

Đồng thời chuyển Group vào ô Grouping Variable, nhấn nút Define Groups và phân chia nhóm với Group 1: 0 ; Group 2: 1. Nhấn Continue và sau đó nhấn OK.

Từ đây ta sẽ có kết quả output bao gồm 3 bảng:

• Bảng Descriptive Statistic: Bảng này không cung cấp cho chúng ta thông tin quan trọng này, vì vậy chúng ta không thể so sánh bất kỳ sự khác biệt nào có thể có giữa các nhóm tập thể dục và ăn kiêng. 
• Việc chưa thử nghiệm để xem liệu sự kết hợp của hai nhóm có dẫn đến việc nhóm lớn hơn được phân phối bình thường hay không. 
• Vì vậy không nên sử dụng giá trị trung bình và độ lệch chuẩn hay phạm vi trung vị và liên phần (IQR). IQR là phân vị thứ 25 đến 75, dẫn đến độ lệch chuẩn cao trong nghiên cứu. Vì những lý do này, bạn nên bỏ qua bảng này.

• Bảng Rank: bảng đầu tiên cung cấp thông tin liên quan đến kết quả của bài kiểm tra Mann-Whitney U. Nó hiển thị thứ hạng trung bình và tổng thứ hạng cho hai nhóm được kiểm tra.

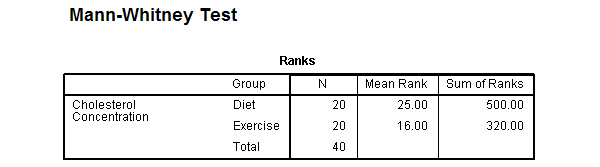
Bảng trên rất hữu ích vì nó cho biết nhóm nào có thể được coi là có nồng độ cholesterol cao hơn, về tổng thể; cụ thể là nhóm có thứ hạng trung bình cao nhất. Trong trường hợp này, nhóm ăn kiêng có nồng độ cholesterol cao nhất.

• Bảng Test Statistics: Bảng này cho chúng ta thấy giá trị ý nghĩa thực tế của thử nghiệm. Cụ thể, bảng Thống kê thử nghiệm cung cấp thống kê thử nghiệm, thống kê U, cũng như giá trị p-có ý nghĩa tiệm cận (2 phía).

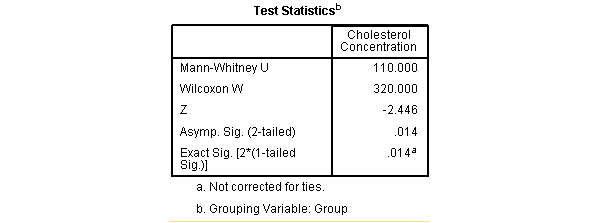
Từ dữ liệu này, có thể kết luận rằng nồng độ cholesterol trong nhóm ăn kiêng cao hơn có ý nghĩa thống kê so với nhóm tập thể dục (U = 110, p = 0,014). Tùy thuộc vào quy mô nhóm của bạn, Thống kê SPSS sẽ tạo ra cả mức ý nghĩa thống kê chính xác và tiệm cận. 

• Cách kiểm định dấu và hạng Wilcoxon: là phép kiểm định so sánh thống kê giá trị trung bình của hai mẫu phụ thuộc. Phép thử kiểm định dấu và Wilcoxon có tương đồng với phép thử t. Trên thực tế, nó là một phương án thay thế mức không liên tục cho phép thử t của các mẫu phụ thuộc.

Ví dụ: Một nhà nghiên cứu về cơn đau quan tâm đến việc tìm ra các phương pháp giảm đau thắt lưng ở từng cá nhân mà không cần phải sử dụng thuốc. Nhà nghiên cứu cho rằng châm cứu vùng thắt lưng có thể giảm đau lưng. Để điều tra điều này, nhà nghiên cứu tuyển 25 người tham gia vào nghiên cứu của họ. Khi bắt đầu nghiên cứu, nhà nghiên cứu yêu cầu những người tham gia đánh giá mức độ đau lưng của họ trên thang điểm từ 1 đến 10, với 10 cho biết mức độ đau lớn nhất. Sau 4 tuần châm cứu hai lần mỗi tuần, những người tham gia được yêu cầu lại để chỉ ra mức độ đau lưng của họ trên thang điểm từ 1 đến 10, với 10 cho biết mức độ đau lớn nhất. Nhà nghiên cứu muốn hiểu liệu mức độ đau của những người tham gia có thay đổi sau khi họ trải qua châm cứu hay không, vì vậy kiểm định dấu và Wilcoxon được thực hiện.

• Cách thực hiện: Đầu tiên cần nhập dữ liệu vào SPSS gồm 2 biến Pain score Pre (khảo sát cơn đau trước khi châm cứu) và Pain score post (khảo sát cơn đau sau khi châm cứu).
• Thực hiện các bước sau để làm kiểm định: Analyze> Nonparametric Tests> 2 Related Samples. Xuất hiện hộp thoại Two-Related-Samples Tests. Tiếp tục chuyển cả 2 biến Pain score Pre và Pain score post vào ô Test Pairs. Tương tự các phần trên, đánh dấu vào 2 ô kiểm định Wilcoxon và ô kiểm định Sign.  

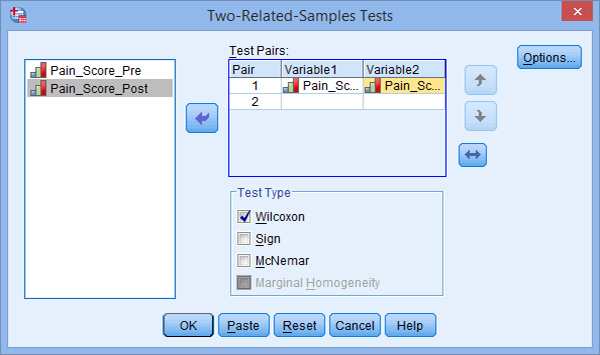
Nhấn OK, cho kết quả gồm 2 bảng sau:

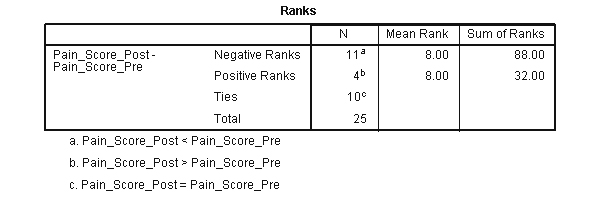
• Bảng Rank: cung cấp một số dữ liệu về việc so sánh  Pain score Pre (Trước) và Pain score post (Sau) của những người tham gia. Chúng ta có thể thấy từ  bảng 11 người tham gia có  Pain score Pre khi điều trị bằng châm cứu cao hơn so với sau khi điều trị. Tuy nhiên, 4 người tham gia có Pain score post hơn sau khi điều trị và 10 người tham gia không thấy thay đổi về  Pain score của họ.

• Bảng Test Statistics: Bằng cách xem xét Bảng Test Statistics thử nghiệm cuối cùng, chúng ta có thể phân tích dữ liệu những thay đổi này, do điều trị bằng châm cứu, nhìn chung có dẫn đến sự khác biệt có ý nghĩa thống kê về Pain scores hay không. Giá trị tìm kiếm “Asymp. Sig. (2 đuôi)”, trong trường hợp này là 0,071. Đây là giá trị p cho phép thử. 

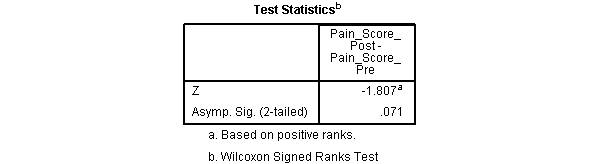
Kết luận: Liệu trình điều trị châm cứu 4 tuần, hai lần mỗi tuần không tạo ra sự thay đổi có ý nghĩa thống kê về chứng đau thắt lưng ở những người bị đau thắt lưng hiện tại (Z = -1,807, p = 0,071). Thật vậy, xếp hạng Pain scores trung bình là 5,0 cả trước và sau khi điều trị.

• Cách kiểm định Kruskall- Wallis: Cách này được sử dụng khi kiểm định sự khác nhau về phân phối từ 3 nhóm trở lên và điều kiện là các phân phối này không có phương sai tương đồng nhau. 

Ví dụ: Các nhà nghiên cứu y học biết rằng một số loại thuốc chống trầm cảm có thể có tác dụng phụ tích cực là giảm đau thần kinh ở những người bị đau lưng mãn tính, thần kinh, khi được sử dụng với liều lượng thấp hơn liều lượng được chỉ định cho bệnh trầm cảm. Các nhà nghiên cứu y học muốn điều tra điều này với một nghiên cứu. Nhà nghiên cứu xác định 3 loại thuốc chống trầm cảm nổi tiếng có thể có tác dụng phụ tích cực này và dán nhãn cho chúng là Thuốc A, Thuốc B và Thuốc C. Sau đó, nhà nghiên cứu tuyển chọn một nhóm gồm 60 người có mức độ đau lưng tương tự và ngẫu nhiên chỉ định họ vào một trong ba nhóm – Nhóm điều trị Thuốc A, Thuốc B hoặc Thuốc C – và kê đơn thuốc liên quan trong thời gian 4 tuần. Vào cuối khoảng thời gian 4 tuần, nhà nghiên cứu yêu cầu những người tham gia đánh giá mức độ đau lưng của họ trên thang điểm từ 1 đến 10, với 10 cho biết mức độ đau lớn nhất. Nhà nghiên cứu muốn so sánh mức độ đau của các nhóm khác nhau khi kết thúc giai đoạn điều trị bằng thuốc. Nhà nghiên cứu chạy thử nghiệm Kruskal-Wallis H để so sánh thước đo thứ tự, phụ thuộc (Pain_Score) này giữa ba phương pháp điều trị bằng thuốc (biến độc lập Drug_Treatment_Group là loại thuốc có nhiều hơn hai nhóm).

Quy trình thực hiện kiểm định: Analyze> Nonparametric Tests> K Independent Samples. Sau đó vào phần Test for Several Independent Samples, ấn vào mục Define Range. Nhấn dấu tick vào ô Minimum số 0 (nhóm 0) và ô Maximum số 2 (nhóm 2).

Phần kết quả output hiển thị như sau:

• Xếp hạng trung bình (tức là cột “Xếp hạng Trung bình” trong bảng Xếp hạng) của Pain_Score cho từng nhóm điều trị bằng thuốc có thể được sử dụng để so sánh hiệu quả của các phương pháp điều trị bằng thuốc khác nhau. Liệu các nhóm điều trị bằng thuốc này có pain score khác nhau hay không có thể được đánh giá bằng cách sử dụng bảng Thống kê Thử nghiệm trình bày kết quả của thử nghiệm Kruskal-Wallis H. 

Kết luận: Có sự khác biệt về ý nghĩa thống kê về pain score giữa các phương pháp điều trị bằng thuốc khác nhau, χ2 (2) = 8.520, p = 0.014, với điểm số đau trung bình là 35,33 đối với Thuốc A, 34,83 đối với Thuốc B và 21,35 cho Thuốc C.

2.2.3. Kiểm định phân phối chuẩn

Kiểm định tham số là các kiểm định mạnh. Tuy nhiên, để sử dụng các kiểm định trên cần thỏa các điều kiện, trong đó có điều kiện tổng thể phải có phân phối chuẩn.

Ví dụ: Dữ liệu của phân phối chuẩn trong SPSS, hiển thị ở chế độ xem dữ liệu với chủ đề nghiên cứu về người nuôi chó (dog ownership) với khoảng cách ném đĩa (Frisbee Throwing Distance in Metres). Cùng xem xét 2 biến này có liên quan với nhau hay không.

Cách thực hiện tính phân phối chuẩn trong SPSS: Vào Analyze -> Descriptive Statistics -> Frequencies. Tại hộp thoại Frequencies hiện lên, chuyển biến read sang ô Variable(s).

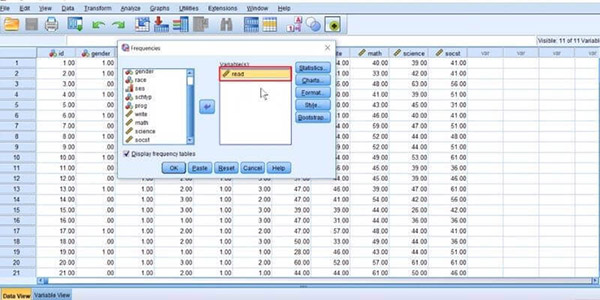
Sau đó nhấn chọn các lệnh theo thứ tự Charts > Histograms > Show normal curve on histogram. Nhấn Continue > OK và chờ kết quả.

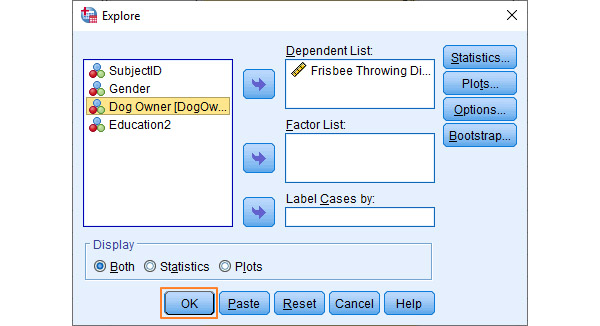
Kết quả hiện ra bảng như sau:

SPSS chạy 2 loại kiểm định phân phối chuẩn: gồm Kolmogorov – Smirnov and Shapiro-Wilk. Từ 2 kết quả trên có thể thấy giá trị đều lớn hơn 0.05, vì vậy có thể bác bỏ giả thuyết H0 là không bình thường.

Có thể thấy khi thực hiện phần kiểm định phân phối chuẩn cũng như các cách kiểm định tham số và phi tham số học viên phải trải qua nhiều bước phức tạp trong SPSS. Để phân tích một cách chính xác các dữ liệu trong nghiên cứu của bạn, chúng tôi có đội ngũ hỗ trợ 24/7 dịch vụ spss chất lượng và nhanh nhất cho bạn

Bài viết trên đây đã chia sẻ những phương pháp chuẩn nhất trong cách kiểm định giả thuyết thống kê trong SPSS kèm những ví dụ cụ thể và chi tiết nhất. Hi vọng bài viết sẽ mang lại những kiến thức bổ ích, giúp bạn thành thạo trong việc sử dụng công cụ SPSS phục vụ cho công việc nghiên cứu của bản thân.